The following is an excerpt from the book NoSQL and SQL Data Modeling: Bringing Together Data, Semantics, and Software by Ted Hills and can be found at https://technicspub.com/nosql/
It turns out that it can be very helpful to separate the two functions of a programming language or DBMS type, namely the specification of a constraint on values and the specification of memory or storage requirements. This separation preserves both terms as very useful, but by clearly focusing each term on only one meaning, thought and communication about data, semantics, and software becomes much clearer and more powerful.
As we have seen in a previous chapter. the term “class”, when properly understood, can be used to describe the composition and “behavior” of computer objects—that is, software objects and hardware objects—all the way down to the level of the hardware objects of which computers are composed. We will preserve this use of “class”.
Classes therefore can be used to specify storage allocation requirements. We will remove this aspect of types, and limit types to designating sets of things—that is, sets of concepts or objects. Types become our means to specify the values that are to be represented in storage, without any presuppositions about how much storage will be needed or how those representations will be constructed.
A class indicates the meaning of the physical states of its objects by declaring that it represents a type. A class represents a type if its objects are designed so that each state of an object represents a member of the set designated by the type.
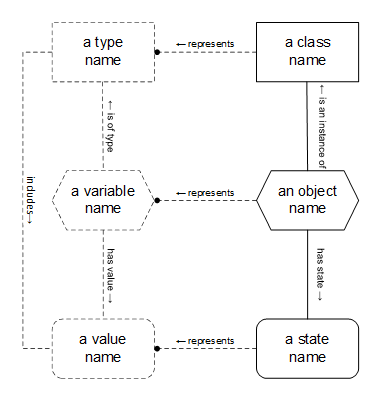
That’s a mouthful, and a lot to remember, so let’s draw that in COMN (Concept and Object Modeling Notation). See Figure 1. Starting at the top of the drawing, we see two rectangles with a line connecting them. The solid rectangle on the right represents a class, and the dashed rectangle on the left represents a type. In COMN, classes are drawn as rectangles using solid lines, in an allusion to the solidity of matter, while types are drawn as rectangles using dashed lines, to indicate that they are conceptual, not physical.
Figure 1. Representation Relationships (The relationship labels are unnecessary.)
The line from class to type with the solid ball on one end expresses the assertion that this class represents this type. The small arrow to the left of the word “represents” indicates the reading direction. Since a line with a ball on the end always indicates a representation relationship in COMN, the word “represents” isn’t actually necessary. It’s just included in this diagram to help you remember what that kind of line means. Because the representation relationship is conceptual and not physical, it is drawn with a dashed line.
In the middle of the diagram we have two hexagons also connected with a representation relationship. We saw the solid hexagon in chapter 10. It represents a software object. The dashed hexagon represents a variable in a program or a field declaration (perhaps a table column, perhaps a document component) in a database. This diagram says that the object represents the variable. In other words, something solid and material, capable of having multiple physical states, represents something symbolic that is declared to be able to take on any of the values of its type. It is usually a compiler or DBMS that allocates an object to represent the variable or field specified symbolically by a programmer or database designer.
At the bottom of this diagram we have two rounded rectangles. The solid-outline rounded rectangle on the right represents a physical state of the object above it. The dashed-outline rounded rectangle on the left represents a value of the type, to which the variable above it is bound. This, finally, shows the mapping of an otherwise meaningless physical state to a value of a type. The declaration that the class at the top represents the type at the top is only valid if in fact every possible state of any of the class’s objects represents a value of the type.
By this means, the representation mapping expresses the meaning of the states of otherwise meaningless objects.
The unadorned lines in this figure (all of which happen to be vertical) have meanings based on the symbols they connect:
- The line from object to class indicates that the object is an instance of the class.
- The line from object to state indicates that the object may have the state.
- The line from variable to type indicates that the variable has the type.
- The line from variable to value indicates that the variable is bound to the value.
- The line on the far left, from type to value, indicates that the type includes the value.
Again, in the case of the unadorned lines, the words are not needed, as there is only one possible interpretation for these lines. Lines in COMN drawings either have a meaning given by arrowheads and tails, such as the ball at the head of the “represents” line, have a meaning given by what they connect, such as the unadorned lines connecting dissimilar symbols, or have a meaning given explicitly in words and other symbols. We will see examples of these later.
Connecting lines are dashed or solid based on whether the relationships they represent are conceptual (dashed) or physical (solid). Any relationship involving something conceptual must itself be conceptual. Relationships between physical things may be physical, but may also be merely conceptual.
Computer objects are physical, and their states are physical phenomena, but descriptions of computer objects—that is, software and DBMS classes—are conceptual. Nonetheless, we draw classes in solid outline to indicate that they are descriptions of physical things.
What is gained by the separation of type and class? Exactly what the world of computer science has been striving for decades, through modeling notations, high-level programming languages, data languages, virtual machines, and other means that have never quite achieved these goals:
- Specification of the “what” independent of the “how”: Existing modeling notations, programming languages, and data languages have tried to enable the expression of software and data requirements independent of particular computer architectures, but the fact that the most basic types assumed some particular representation meant they always failed. A virtual machine is not devoid of such assumptions: it simply specifies a particular set of representation assumptions independent of any real computer (even including the arbitrary choice of endian-ness). In contrast, COMN can truly describe the “what” in terms of types independently of any assumed virtual or real representations.
- Description of the “how” independent of the “what”: Classes can be used to describe the mechanisms and states of raw computer hardware before any meaning has been attached to those states. Most modeling notations and high-level programming languages cannot express ideas at this low level.
- Specification of the representation of requirements separately from specification of the requirements: Once a pure description of the “what” has been drawn in COMN, the design of the “how” can be completed by building up classes and objects from those available on the implementation platform, and those classes and objects can be mapped to the types in the requirements using representation mappings. Most existing notations and languages cannot express this mapping, either because they’ve tangled the concept of types with assumed representations and implementations, or they’ve prohibited the expression of implementation concerns, or (strangely but commonly) both.
